Introduction: The Lotka-Volterra model is composed of a pair of differential equations that describe predator-prey (or herbivore-plant, or parasitoid-host) dynamics in their simplest case (one predator population, one prey population). It was developed independently by Alfred Lotka and Vito Volterra in the 1920's, and is characterized. Goodstein, J.R.: The Volterra Chronicles, The Life and Times of an Extraordinary Mathematician 1860–1940.American Mathematical Society (2007).
- The Lotka-Volterra ODE system: d x d t = α x − β x y. D y d t = δ x y − γ y with initial values for x = 10 and y = 10. The parameter values for alpha, beta, delta and gamma are 1.1, 0.4, 0.1 and 0.4 respectively (mimicking this example).
- Discrete-time Lotka-Volterra model: V t+1 = rV t aP tV t P t+1 = sP t + acP tV t V is prey (victim'), P is predator. R is prey growth rate; a is attack rate of predators; c is conversion e ciency of predators; s is predator survival in the.
In this post, I’ll explore using R to analyze dynamical systems. Using the Lotka-Volterra predator prey model as a simple case-study, I use the R packages deSolve to solve a system of differential equations and FME to perform a sensitivity analysis.
Lotka-Volterra model
The Lotka-Volterra model describes the dynamics of a two-species system in which one is a predator and the other is its prey. The equations governing the dynamics of the prey (with density (x) and predator (with density (y)) are:
[begin{aligned} frac{dx}{dt} & = alpha x - beta xy frac{dy}{dt} & = delta beta xy - gamma y end{aligned}]
where (alpha) is the (exponential) growth rate of the prey in the absence of predation, (beta) is the predation rate or predator search efficiency, (delta) describes the predator food conversion efficiency, and (gamma) is the predator mortality.
Solving the ODE
Given a set of initial conditions and parameter estimates, deSolve::ode() can be used to evolve a dynamical system described by a set of ODEs. I start by defining parameters, as a named list, and the initial state, as a vector. For the initial state, it is the order that matters not the names.
Next, I need to define a function that computes the derivatives in the ODE system at a given point in time.
The vignette for FME suggets rolling all this into a function as follows. This function will become the input for the FME sensitivity analysis.
The ouput of ode() is a matrix with one column for each state variable. I convert this to a data frame and plot the evolution of the system over time.
This choice of paramters leads to periodic dynamics in which the prey population initially increases, leading to an abundance of food for the predators. The predators increase in response (lagging the prey population), eventually overwhelming the prey population, which crashes. This in turn causes the predators to crash, and the cycle repeats. The period of these dynamics is about 15 seconds, with the predators lagging the prey by about a second.
Sensitivity analysis
A sensitivity analysis examines how changes in the parameters underlying a model affect the behaviour of the system. It can help us understand the impact of uncertainty in parameter estimates. The FME vignette covers two types of sensitivity analyses: global and local.
Global sensitivity
According to the FME vingette, in a global sensitivity analysis certain parameters (the sensitivity parameters) are varied over a large range, and the effect on model output variables (the sensitivity variables) is measured. To accomplish this, a distribution is defined for each sensitivity parameter and the model is run multiple times, each time drawing values for the sensistivity parameters from their distribution. The sensitivity variables are recorded for each iteration over a range of times. The function sensRange() carries out global sensitivity analyses.
I’ll look at the sensitivity of the populations to the growth rate ((alpha)) and the predation rate ((beta)). Defining the sensitivity parameter distributions requires providing a data frame in which the first column is the minimum value, the second column the maximum, and the row names are the parameter names.

Now I use sensRange() to solve the models over the range of parameters. The argument dist = 'grid' sets the sensitivity parameter distribution to a regular grid of values, sensvar defines which variables are the sensitivity variables (i.e. the ones whose time series will be returned in the output), num is the number of iterations and therefore the number of different sensistivity parameter values (note that if there are (k) sensitivity parameters, num must have an integer (k)th root), and times is the time series over which to evaluate the model.
The output of this function is a data frame with rows corresponding to the different sensitivity parameter values and columns corresponding to the combination of time steps and sensitivity variables. So, for n time steps, there are n columns for each sensitivity variable. First I run a simple sensitivity analysis to aid examination of the output.
Here variables such as x0.5 refer to the values of (x) at (t=0.5). FME provides a plot() method for sensRange objects, which adds envelopes to the variables showing the range and mean ± standard deviation. Now I run a more realistic sensitivity analysis and produce the plots. Note that summary() must be called before plot() to get the desired plots.
To actually work with these data, I’ll transform the data frame from wide to long format using tidyr. gather() converts from wide to long format, then separate() splits column names x1.5 into two fields: one identifying the variable (x) and one specifying the time step (1.5).
Now, I can, for example, recreate the above plot with ggplot2. First, I summarize the data to calculate the envelopes, then I plot.
In this format, it’s also easy to fix one of the values for a sensitivity parameter and only vary the other one.
Local sensitivity analysis
According to the FME vingette, in a local sensitivity analysis, “the effect of a parameter value in a very small region near its nominal value is estimated”. The method used by FME is to calculate a matrix of sensitivity functions, (S_{i,j}), defined by:
[S_{i,j} = f(v_i, p_i) = frac{dv_i}{dp_j} frac{s_{p_j}}{s_{v_i}}]
where (v_i) is a sensitivity variable (i) (which is dependent on time (t)), (p_j) is sensitivity parameter (j), and (s_{v_i}) and (s_{p_j}) are scaling factors for variables and parameters, respectively. By default, FME takes the scaling values to be equal to the underlying quantities, in which case the above equation simplifies to:
[S_{i,j} = f(v_i, p_i) = frac{dv_i}{dp_j} frac{p_j}{v_i}]
The function sensFun() is used to numerically estimate these sensitivity functions at a series of time steps. The arguments sensvar and senspar are used to define which variables and parameters, respectively, will be investigated in the sensitivity analysis. By default, all variables are parameters are included. The arguments varscale and parscale define the scaling factors; however, for now, I’ll leave them blank, which sets them to the underlying quantities as in the above equation.
In practice, sensFun() works by applying a small perturbation, (delta_j), to parameter (j), solving the model for a range of time steps to determine (v_i), then taking the ratio of the changes to the parameters and variables. The perturbation is defined by the argument tiny as (delta_j = text{max}(tiny, tiny * p_j)). tiny defaults to (10^{-8}).
To test that sensFun() is doing what I think it is, I’ll implement a version of it. For simplicity, I’ll only consider the variable (x) (prey density):
Now I compare this implementation to the actual results.
A perfect match! Now that I know what sensFun() is actually doing, I’ll put it to use to solve the original LV model. One difference here is that I’ll consider both variables as sensitivity variables and the results for each variable will be stacked rowwise. In addition, in the FME documentation, (s_{v_i}) is set to 1, which is on the order of the actual variable values, but has the benefit of being constant over time. I’ll do the same here.
Lotka Volterra 1925
summary() can be used to summarize these results over the time series, for example, to see which parameters the model is most sensitive too.
(gamma) (predator mortality rate) and (beta) (predator search efficiency) have the largest values for the sensitivity function, on average, suggesting that this model is most sensitive to these parameters. There is also plot method for the output of sensFun(), which plots the sensitivity functions as time series.
However, it’s also possible to use ggplot2 provided I transpose the data to long format first.
Clearly this model is particularly sensitive to (gamma). Furthermore, this sensitivity shows peaks every 16 seconds or so, which is the periodicity of the original dynamics. To see what’s going on here, I’ll take a look at what happens to the two species when I increase (gamma) by 1%:
Increasing (gamma) leads to a time dependent period to the dynamics. As a result, the two models initially overlap, but they become increasingly out of sync over time. This explains both the periodicity of the sensitivity function and the increasing amplitude.
Related
Introduction: The Lotka-Volterra model is composed of a pairof differential equations that describe predator-prey (or herbivore-plant,or parasitoid-host) dynamics in their simplest case (one predator population,one prey population). It was developed independently by Alfred Lotka andVito Volterra in the 1920's, and is characterized by oscillations in thepopulation size of both predator and prey, with the peak of the predator'soscillation lagging slightly behind the peak of the prey's oscillation.The model makes several simplifying assumptions: 1) the prey populationwill grow exponentially when the predator is absent; 2) the predator populationwill starve in the absence of the prey population (as opposed to switchingto another type of prey); 3) predators can consume infinite quantitiesof prey; and 4) there is no environmental complexity (in other words, bothpopulations are moving randomly through a homogeneous environment).
Importance: Predators and prey can influenceone another's evolution. Traits that enhance a predator's ability to findand capture prey will be selected for in the predator, while traits thatenhance the prey's ability to avoid being eaten will be selected for inthe prey. The 'goals' of these traits are not compatible, and it is theinteraction of these selective pressures that influences the dynamics ofthe predator and prey populations. Predicting the outcome of species interactionsis also of interest to biologists trying to understand how communitiesare structured and sustained.
Question: What are the predictions of theLotka-Volterra model? Are they supported by empirical evidence?
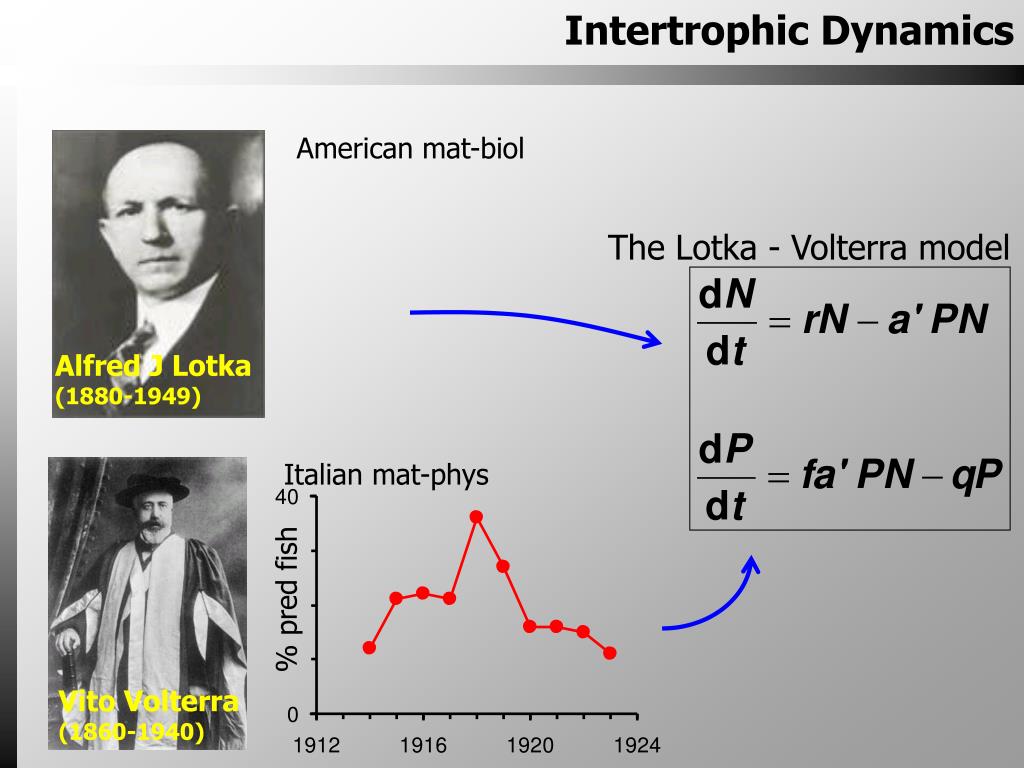
Variables:| P | number of predators or consumers |
| N | number of prey or biomassof plants |
| t | time |
| r | growth rate of prey |
| a' | searching efficiency/attackrate |
| q | predator or consumer mortalityrate |
| c | predatorís or consumerísefficiency at turning food into offspring (conversion efficiency) |
Methods: We begin by looking at whathappens to the predator population in the absence of prey; without foodresources, their numbers are expected to decline exponentially, as describedby the following equation:
.
This equation uses the product of the number of predators(P) and the predator mortality rate (q) to describe the rateof decrease (because of the minus sign on the right-hand side of the equation)of the predator population (P) with respect to time (t).In the presence of prey, however, this decline is opposed by the predatorbirth rate, caíPN, which is determined by the consumption rate (aíPN,which is the attack rate[a'] multiplied by the product of the numberof predators [P] times the number of prey [N]) and by thepredatorís ability to turn food into offspring (c). As predatorand prey numbers (P and N, respectively) increase, theirencounters become more frequent, but the actual rate of consumption willdepend on the attack rate (aí). The equation describing the predatorpopulation dynamics becomes.
Turning to the prey population, we would expect thatwithout predation, the numbers of prey would increase exponentially. Thefollowing equation describes the rate of increase of the prey populationwith respect to time, where r is the growth rate of the prey population,and N is the abundance of the prey population:
.
Lotka Volterra Graphs
In the presence of predators, however, the prey populationis prevented from increasing exponentially. The term for consumption ratefrom above (aíPN) describes prey mortality, and the population dynamicsof the prey can be described by the equation.
Equations (2) and (4) describe predator and preypopulation dynamics in the presence of one another, and together make upthe Lotka-Volterra predator-prey model. The model predicts a cyclical relationshipbetween predator and prey numbers: as the number of predators (P)increases so does the consumption rate (a'PN), tending to reinforcethe increase in P. Increase in consumption rate, however, has anobvious consequence-- a decrease in the number of prey (N), whichin turn causes P (and therefore a'PN) to decrease. As a'PNdecreases the prey population is able to recover, and N increases.Now P can increase, and the cycle begins again. This graph showsthe cyclical relationship predicted by the model for hypothetical predatorand prey populations.
Huffaker (1958) reared two species of mites to demonstratethese coupled oscillations of predator and prey densities in the laboratory.Using Typhlodromus occidentalis as the predator and the six-spottedmite (Eotetranychus sexmaculatus) as the prey, Huffaker constructedenvironments composed of varying numbers of oranges (fed on by the prey)and rubber balls on trays. The oranges were partially covered with waxto control the amount of feeding area available to E. sexmaculatus,and dispersed among the rubber balls. The results of one of the many permutationsof his experiments are graphed below. Note that the prey population sizeis on the left vertical axis and the predator population is on the rightvertical axis, and that the scales of the two are different (after Huffaker,1958 [fig.18]).
Interpretation: It is apparent from the graphthat both populations showed cyclical behavior, and that the predator populationgenerally tracked the peaks in the prey population. However, there is someinformation about this experiment that we need to consider before concludingthat the experimental results truly support the predictions made by theLotka-Volterra model. To achieve the results graphed here, Huffaker addedconsiderable complexity to the environment. Food resources for E. sexmaculatus(the oranges), were spread further apart than in previous experiments,which meant that food resources for T. occidentalis (i.e., E.sexmaculatus) were also spread further apart. Additionally, the orangeswere partially isolated with vaseline barriers, but the prey's abilityto disperse was facilitated by the presence of upright sticks from whichthey could ride air currents to other parts of the environment. In otherwords, predator and prey were not encountering one another randomly inthe environment (see assumption 4 from the Introduction).
Conclusions: A good model must be simple enoughto be mathematically tractable, but complex enough to represent a systemrealistically. Realism is often sacrificed for simplicity, and one of theshortcomings of the Lotka-Volterra model is its reliance on unrealisticassumptions. For example, prey populations are limited by food resourcesand not just by predation, and no predator can consume infinite quantitiesof prey. Many other examples of cyclical relationships between predatorand prey populations have been demonstrated in the laboratory or observedin nature, but in general these are better fit by models incorporatingterms that represent carrying capacity (the maximum population size thata given environment can support) for the prey population, realistic functionalresponses (how a predator's consumption rate changes as prey densitieschange) for the predator population, and complexity in the environment.
Additional Question:
1) How would increases or decreases in any of theparameters r, q, a', or c affect the rate ofchange of either the predator or prey populations? How would the shapeof the graph change?
Sources: Begon, M., J. L. Harper, and C. R.Townsend. 1996. Ecology: Individuals, Populations, and Communities,3rd edition. Blackwell Science Ltd. Cambridge, MA.
Gotelli, N. J. 1998. A Primer of Ecology,2nd edition. Sinauer Associates, Inc. Sunderland, MA.
Lotka Volterra Equation Explained
Huffaker, C. B. 1958. Experimental studies on predation:dispersion factors and predator-prey oscillations. Hilgardia 27(14):343-383.
copyright 1999, M. Beals, L. Gross, and S. Harrell